CÁLCULO II


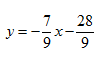
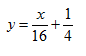
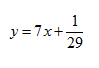












A partir de uma folha de papelão quadrada de lado 30 cm deseja-se construir uma caixa sem tampa. Para construir a caixa serão recortados quatro quadrados nos cantos desta folha, conforme mostra a figura, dobrando-se a folha nas linhas tracejadas para formar as laterais da caixa. Encontre o valor da dimensão x deste quadrado de modo que o volume da caixa seja máximo.

O recorte deve ter 6,3 cm.
O recorte deve ter 4,0 cm.
O recorte deve ter 7,0 cm.
O recorte deve ter 5,0 cm.
O recorte deve ter 5,8 cm.
Um homem com 2 m de altura está correndo à velocidade de 3 m/s e passa embaixo de uma lâmpada num poste a 6 m acima do solo. Qual a velocidade com que o topo de sua sombra se move?

A velocidade com que o topo da sombra se move é 4,5 m/s.
A velocidade com que o topo da sombra se move é 5,4 m/s.
A velocidade com que o topo da sombra se move é 2,4 m/s.
A velocidade com que o topo da sombra se move é 1,7 m/s.
A velocidade com que o topo da sombra se move é 3,5 m/s.


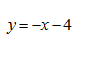












A partir de uma folha de papelão quadrada de lado 30 cm deseja-se construir uma caixa sem tampa. Para construir a caixa serão recortados quatro quadrados nos cantos desta folha, conforme mostra a figura, dobrando-se a folha nas linhas tracejadas para formar as laterais da caixa. Encontre o valor da dimensão x deste quadrado de modo que o volume da caixa seja máximo.

O recorte deve ter 6,3 cm.
O recorte deve ter 4,0 cm.
O recorte deve ter 7,0 cm.
O recorte deve ter 5,0 cm.
O recorte deve ter 5,8 cm.
Um homem com 2 m de altura está correndo à velocidade de 3 m/s e passa embaixo de uma lâmpada num poste a 6 m acima do solo. Qual a velocidade com que o topo de sua sombra se move?

A velocidade com que o topo da sombra se move é 4,5 m/s.
A velocidade com que o topo da sombra se move é 5,4 m/s.
A velocidade com que o topo da sombra se move é 2,4 m/s.
A velocidade com que o topo da sombra se move é 1,7 m/s.
A velocidade com que o topo da sombra se move é 3,5 m/s.













A partir de uma folha de papelão quadrada de lado 30 cm deseja-se construir uma caixa sem tampa. Para construir a caixa serão recortados quatro quadrados nos cantos desta folha, conforme mostra a figura, dobrando-se a folha nas linhas tracejadas para formar as laterais da caixa. Encontre o valor da dimensão x deste quadrado de modo que o volume da caixa seja máximo.

O recorte deve ter 6,3 cm.
O recorte deve ter 4,0 cm.
O recorte deve ter 7,0 cm.
O recorte deve ter 5,0 cm.
O recorte deve ter 5,8 cm.
Um homem com 2 m de altura está correndo à velocidade de 3 m/s e passa embaixo de uma lâmpada num poste a 6 m acima do solo. Qual a velocidade com que o topo de sua sombra se move?

A velocidade com que o topo da sombra se move é 4,5 m/s.
A velocidade com que o topo da sombra se move é 5,4 m/s.
A velocidade com que o topo da sombra se move é 2,4 m/s.
A velocidade com que o topo da sombra se move é 1,7 m/s.
A velocidade com que o topo da sombra se move é 3,5 m/s.







A partir de uma folha de papelão quadrada de lado 30 cm deseja-se construir uma caixa sem tampa. Para construir a caixa serão recortados quatro quadrados nos cantos desta folha, conforme mostra a figura, dobrando-se a folha nas linhas tracejadas para formar as laterais da caixa. Encontre o valor da dimensão x deste quadrado de modo que o volume da caixa seja máximo.

O recorte deve ter 6,3 cm.
O recorte deve ter 4,0 cm.
O recorte deve ter 7,0 cm.
O recorte deve ter 5,0 cm.
O recorte deve ter 5,8 cm.
Um homem com 2 m de altura está correndo à velocidade de 3 m/s e passa embaixo de uma lâmpada num poste a 6 m acima do solo. Qual a velocidade com que o topo de sua sombra se move?

A velocidade com que o topo da sombra se move é 4,5 m/s.
A velocidade com que o topo da sombra se move é 5,4 m/s.
A velocidade com que o topo da sombra se move é 2,4 m/s.
A velocidade com que o topo da sombra se move é 1,7 m/s.
A velocidade com que o topo da sombra se move é 3,5 m/s.

A partir de uma folha de papelão quadrada de lado 30 cm deseja-se construir uma caixa sem tampa. Para construir a caixa serão recortados quatro quadrados nos cantos desta folha, conforme mostra a figura, dobrando-se a folha nas linhas tracejadas para formar as laterais da caixa. Encontre o valor da dimensão x deste quadrado de modo que o volume da caixa seja máximo.

O recorte deve ter 6,3 cm.
O recorte deve ter 4,0 cm.
O recorte deve ter 7,0 cm.
O recorte deve ter 5,0 cm.
O recorte deve ter 5,8 cm.
Um homem com 2 m de altura está correndo à velocidade de 3 m/s e passa embaixo de uma lâmpada num poste a 6 m acima do solo. Qual a velocidade com que o topo de sua sombra se move?

A velocidade com que o topo da sombra se move é 4,5 m/s.
A velocidade com que o topo da sombra se move é 5,4 m/s.
A velocidade com que o topo da sombra se move é 2,4 m/s.
A velocidade com que o topo da sombra se move é 1,7 m/s.
A velocidade com que o topo da sombra se move é 3,5 m/s.

O recorte deve ter 6,3 cm.
O recorte deve ter 4,0 cm.
O recorte deve ter 7,0 cm.
O recorte deve ter 5,0 cm.
O recorte deve ter 5,8 cm.
Um homem com 2 m de altura está correndo à velocidade de 3 m/s e passa embaixo de uma lâmpada num poste a 6 m acima do solo. Qual a velocidade com que o topo de sua sombra se move?

A velocidade com que o topo da sombra se move é 4,5 m/s.
A velocidade com que o topo da sombra se move é 5,4 m/s.
A velocidade com que o topo da sombra se move é 2,4 m/s.
A velocidade com que o topo da sombra se move é 1,7 m/s.
A velocidade com que o topo da sombra se move é 3,5 m/s.

A velocidade com que o topo da sombra se move é 4,5 m/s.
A velocidade com que o topo da sombra se move é 5,4 m/s.
A velocidade com que o topo da sombra se move é 2,4 m/s.
A velocidade com que o topo da sombra se move é 1,7 m/s.
A velocidade com que o topo da sombra se move é 3,5 m/s.